Cette nouvelle tuile « Einstein » peut faire quelque chose qu’aucune autre forme ne peut réaliser

Ce polygone en forme de chapeau peut couvrir un espace infini et ne jamais se répéter une seule fois.

Einstein a encore frappé. Non, pas cette fois, « l’einstein » qui a changé le monde des mathématiques et de la physique est un minuscule polygone oblique qu’on a surnommé « le chapeau ».

Il n’y a aucun rapport avec le célèbre physicien : dans ce cas, « einstein » vient de l’allemand « ein Stein », qui signifie « une pierre », et c’est un nom assez approprié pour la petite forme spéciale. 

C’est parce que « le chapeau » peut faire quelque chose qu’aucune autre forme connue ne peut faire : il s’articule avec lui-même de telle manière qu’il peut couvrir une surface infinie sans jamais créer de motif répétitif.

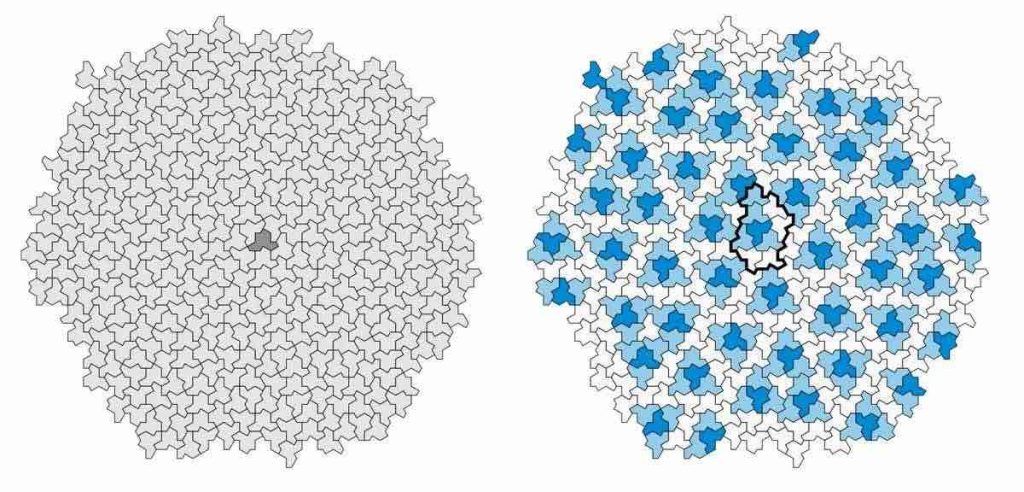
Un patch de 10 de 392 chapeaux généré par ordinateur (à gauche), disposé en dix anneaux concentriques autour d’un chapeau ombré central. Les tuiles peuvent être colorées (à droite), montrant que les chapeaux réfléchis (bleu foncé) sont dispersés et chacun est entouré d’une « coque » congruente de trois chapeaux non réfléchis (bleu clair). Un contour épaissi montre la limite du groupe maximal de tuiles qui apparaît de manière congruente autour de chaque tuile réfléchie. Crédit d’image : Smith et al, 2023,  CC-BY-4.0

C’est une découverte d’environ 50 ans. Le pavage apériodique le plus célèbre – c’est-à-dire un pavage qui ne se répète jamais – a été créé par Roger Penrose en 1974, mais il fallait deux tuiles distinctes pour fonctionner. Depuis lors, cependant, les mathématiciens se demandent : la même chose pourrait-elle être possible en utilisant une seule tuile ?

Aujourd’hui, grâce au mathématicien non professionnel David Smith, ainsi qu’à une équipe de chercheurs universitaires venus du Royaume-Uni et des États-Unis, la réponse a été trouvée.

« Tout le monde est étonné et ravi », a déclaré à Science News Marjorie Senechal, professeure émérite de mathématiques et d’histoire des sciences et technologies au Smith College, qui n’a pas participé à la découverte . « Il n’était même pas clair qu’une telle chose puisse exister. » 

Même en sachant que c’est le cas, la solution s’est avérée d’une simplicité désarmante. Avant que Smith ne vienne vers lui et ses collègues avec la nouvelle forme, « J’aurais dessiné une chose folle, sinueuse et complexe » si on lui avait demandé de suggérer un einstein potentiel, Chaim Goodman-Strauss, professeur de mathématiques à l’Université de l’Arkansas et co -auteur d’une nouvelle prépublication sur la découverte, a déclaré à Science News.

Une autre vue des chapeaux en pavage, mettant en évidence sa construction à partir de huit petits polygones en forme de cerf-volant. Crédit d’image : Smith et al, 2023,  CC-BY-4.0 

Bien que le document n’ait pas encore été examiné par des pairs, les experts estiment qu’il est susceptible de résister à un examen minutieux. Trouver la tuile et prouver son apériodicité a nécessité l’utilisation à la fois d’ordinateurs puissants et de créativité humaine, a déclaré Goodman-Strauss au New Scientist :

« Vous recherchez littéralement une chose sur un million. Vous filtrez les 999 999, puis vous avez quelque chose de bizarre, et cela mérite une exploration plus approfondie », a-t-il expliqué. 

« Et puis à la main, vous commencez à les examiner et essayez de les comprendre, et commencez à retirer la structure », a-t-il ajouté. « C’est là qu’un ordinateur serait sans valeur car un humain devait être impliqué dans la construction d’une preuve qu’un humain pourrait comprendre. »

Cette preuve, dans sa forme la plus élémentaire, comportait deux étapes. Le premier indice que les « chapeaux » étaient quelque chose de spécial était leur tendance à s’organiser en groupes plus grands, ou « métatiles ». Celles-ci, à leur tour, s’organisent en « supertiles » encore plus grandes, et ainsi de suite – un comportement courant dans les pavages non périodiques, et était un indice majeur que la forme pourrait être un einstein potentiel.

Cependant, prouver son apériodicité nécessitait une technique légèrement différente. Pour cela, l’équipe a étiré et transformé le chapeau pour créer une famille de tuiles le long d’un continuum – toutes avec le même motif répétitif, mais à différentes étapes entre deux formes extrêmes. En considérant la situation à ces extrêmes, les chercheurs ont pu montrer que le pavage créé par le chapeau était bien apériodique. 

Bien que la nouvelle forme puisse exciter les géomètres, les implications de la découverte d’un véritable einstein s’étendent au-delà du département de mathématiques pures. Les pavages apériodiques sont importants dans le développement des quasi-cristaux , qui à leur tour ont trouvé des applications dans tout, des Kleenexes aux robots réels de style Terminator .

Pour certains, cependant, les utilisations potentielles de la nouvelle forme certes mignonne commencent plus près de chez eux.

« Vous allez voir des gens les mettre dans une salle de bain parce que c’est juste cool », a déclaré Colin Adams, professeur de mathématiques au Williams College, qui n’a pas participé à la recherche. 

« Je le mettrais dans ma salle de bain si je le carrelais en ce moment. »

Le document est disponible serveur de préimpression arXiv .